
The Impact on Relative Mortality and Prevalence From Triage in an Accelerated Underwriting Program
properties.trackTitle
properties.trackSubtitle
Accelerated underwriting programs continue to evolve at a rapid pace. Triage systems have become a key element in many of the newer programs in the market. Depending on the criteria used at the triage point, these programs can have residual effects on class prevalence and mortality, which in turn affect the profitability of these programs. In this article we will explore some potential impacts on mortality and prevalence within the accelerated underwriting programs.
History of accelerated underwriting
In the individual life insurance space, accelerated underwriting (AUW) is the newest iteration of underwriting. In these programs, instead of collecting blood and taking the physical measurements of the applicant, underwriting relies on self-reported measurements along with information from various databases and scoring tools.
AUW 1.0
In early accelerated underwriting programs, companies simply changed their age and amount requirements. For certain ages and face amounts, paramedical exams and fluid testing were replaced with checks on prescription drug (Rx) and motor vehicle records (MVR) databases. The mortality impact of removing fluids was assessed as a load to the company’s fully underwritten mortality assumption that was partially offset by a discount associated with the protective value of the new underwriting tools and expense savings. In addition, because these changes meant that the underwriting decision would be based on self-reported information rather than tested information (e.g., build and smoker status), loads were introduced to account for asymmetry of information and additional adverse selection.
These early programs often passed on the net increase in expected mortality to the end consumer. Also, the first adopters of these programs usually did not allow for preferred risk classes. Thus these programs were not priced competitively and were prone to additional adverse selection. Few, if any, of these programs achieved their sales targets, and the mortality experience was often poor.
AUW 2.0
In order to make these products more attractive to consumers and attract better risks, companies started to introduce various changes. Chart 1 outlines the general evolution of these products over time.
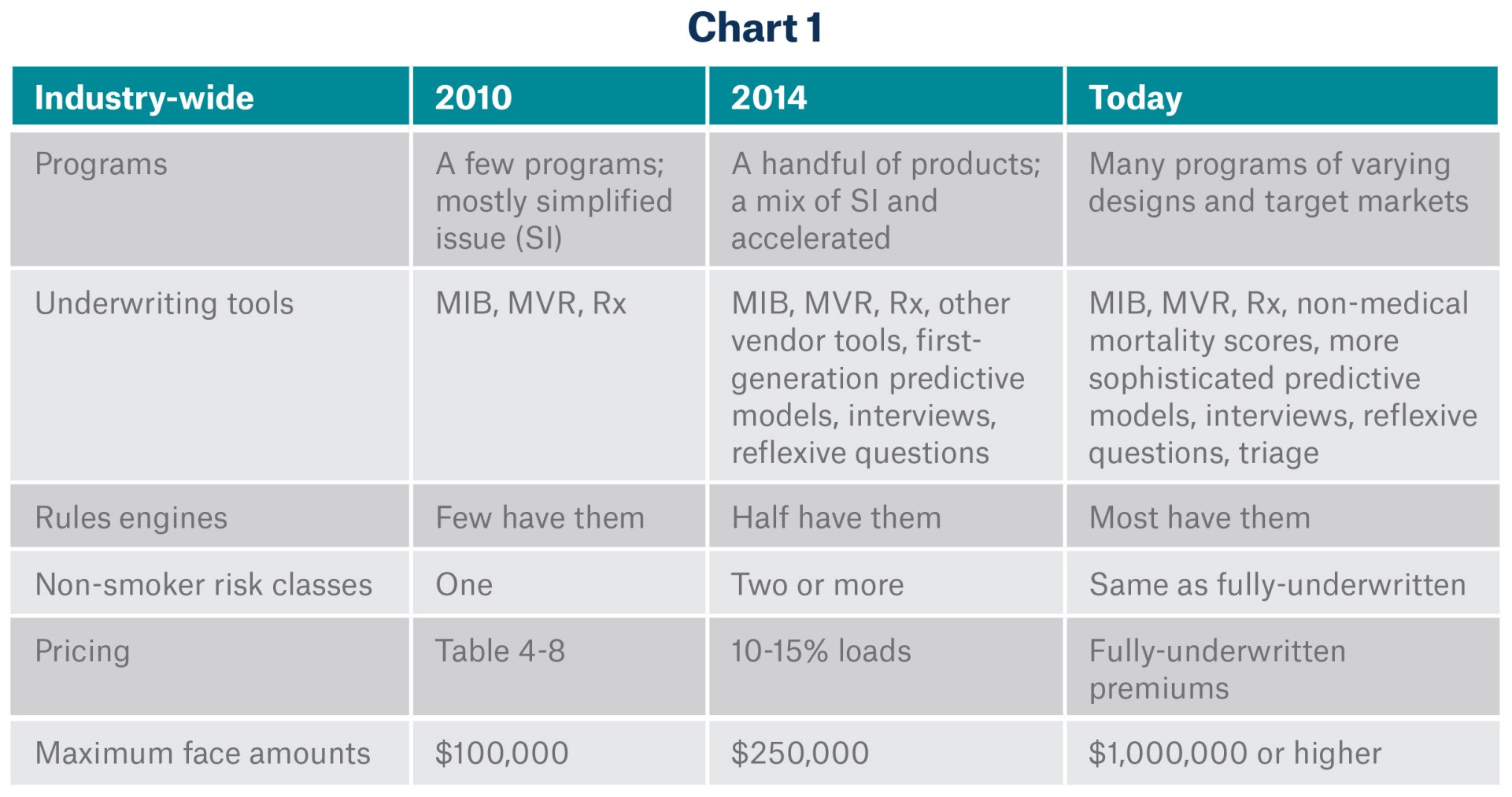
The product parameters and underwriting tools in accelerated underwriting programs continue to evolve. This article will focus on a few aspects related to the use of underwriting triage to select better risks and/or to introduce a sentinel effect.
Triage
“Triage” in this context is the introduction of decision nodes in the underwriting process, where the applicant is evaluated using a subset of the available information that provides predictive value. A major benefit of triage is the ability to restrict the availability of accelerated underwriting to those applicants who represent better risks or where there is a higher degree of confidence of assigning an appropriate risk class. A human underwriter typically steps in for applicants with negative indicators, allowing the company to strike a balance between the expense savings of removing fluid underwriting and the extra cost of mortality due to its loss. An illustration of a simple triage system is presented in Graph 1.
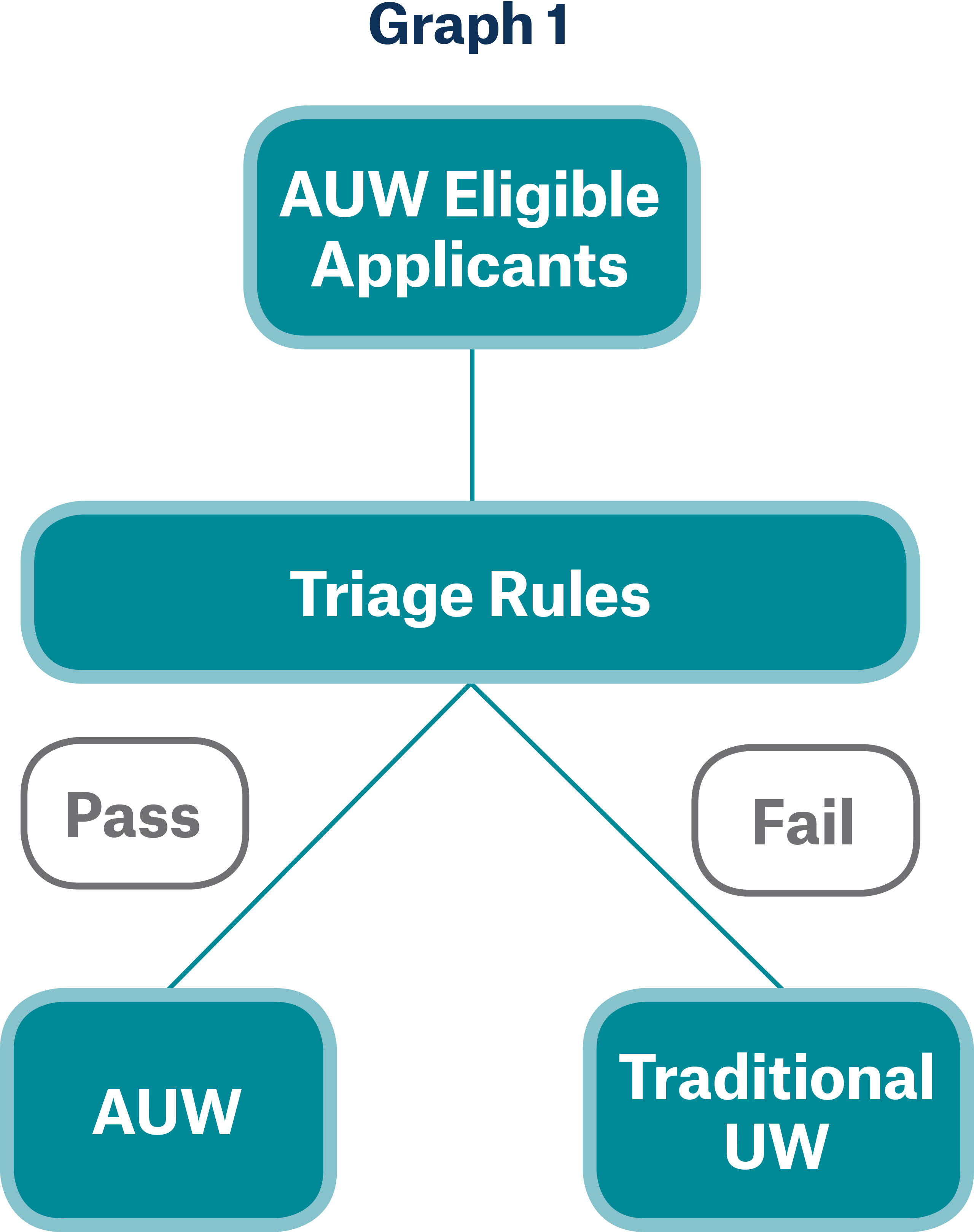
In this simple triage example, thresholds are set based on certain database checks and responses to the application questions. If the applicant meets these thresholds then the application proceeds to accelerated underwriting. If not, the applicant is required to undergo more traditional underwriting.
Examples of criteria used in triage models include the use of non-medical mortality scores or the use of prescription drug database rules or scores, both of which have been shown to segment mortality1,2. As such, the use of triage creates a quasi-preferred class structure. This segmentation can impact both the risk class prevalence and relative mortality on each side of the triage, the degree of which varies with the level of correlation between the triage model’s criteria and the company’s preferred underwriting rules. On this spectrum of correlation, two extremes exist:
1) The triage model is not correlated with the preferred class underwriting rules.
2) The triage model and the preferred rules are highly correlated.
Extreme 1: The triage model is not correlated with preferred class underwriting
Under the first scenario where the triage model’s selection criteria are not correlated with the preferred class underwriting rules but the triage model is predictive of mortality, the pricing mortality assumption would require a path-dependent adjustment: one triage path would have better mortality than the other. However, because this triage model’s criteria are not correlated with preferred underwriting rules, each path should have roughly the same preferred composition3. In other words, if a triage model’s selection criteria are not correlated with preferred underwriting rules, the model can shift mortality relative to full underwriting without affecting preferred class prevalence. Using only a credit-based risk score cutoff for the triage decision while using only health information for the preferred class rules is an example of this extreme. This relationship can be seen in Graph 2 below, which displays class distribution shifts using Lexis Nexis Risk Classifier (LNRC), a credit-based risk score, as triage model:
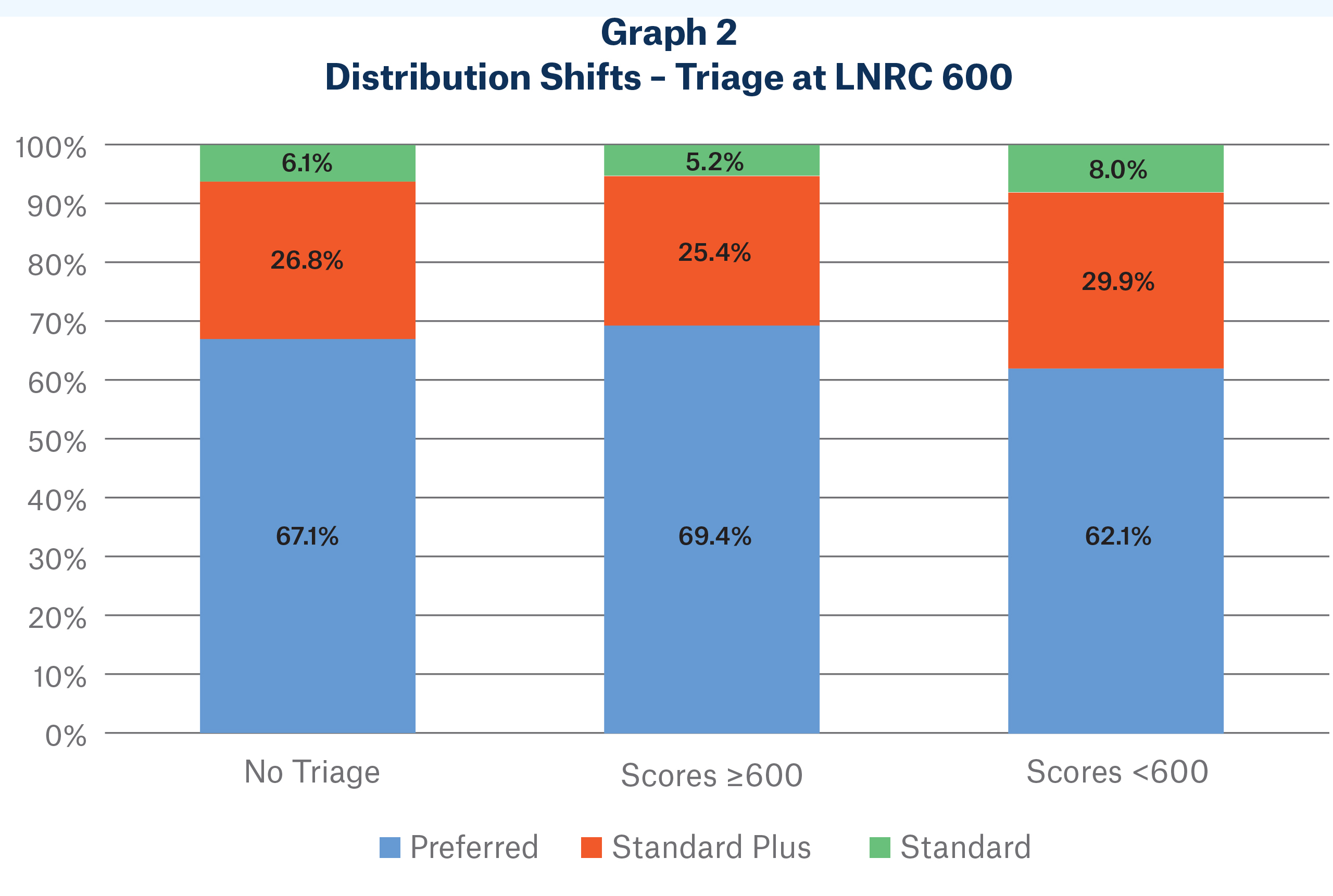
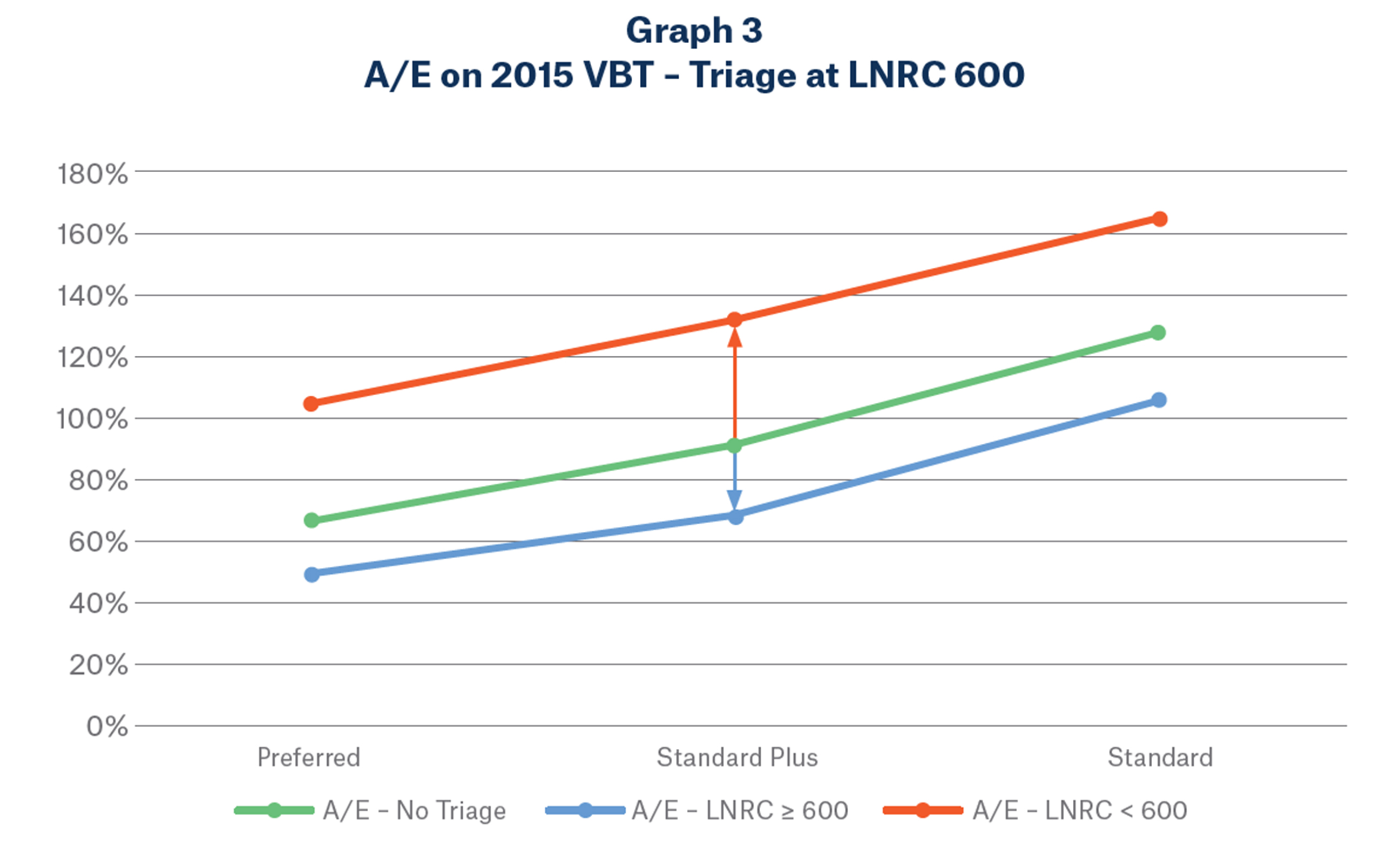
In this example, a fully underwritten sample population of about 500,000 lives were triaged at an LNRC score of 600. Note that the risk class distribution at and above a score of 600 is extremely similar to the distribution below 600. Scores below 600 are slightly biased toward standard traditional risk classes, but this bias is slight. For this population, LNRC score is a weak predictor of underwriting risk class. Despite this, it is strongly predictive of mortality within risk classes. See Graph 3 on next page, which displays how an effective triage model with low correlation to preferred criteria can segment mortality within each risk class4.
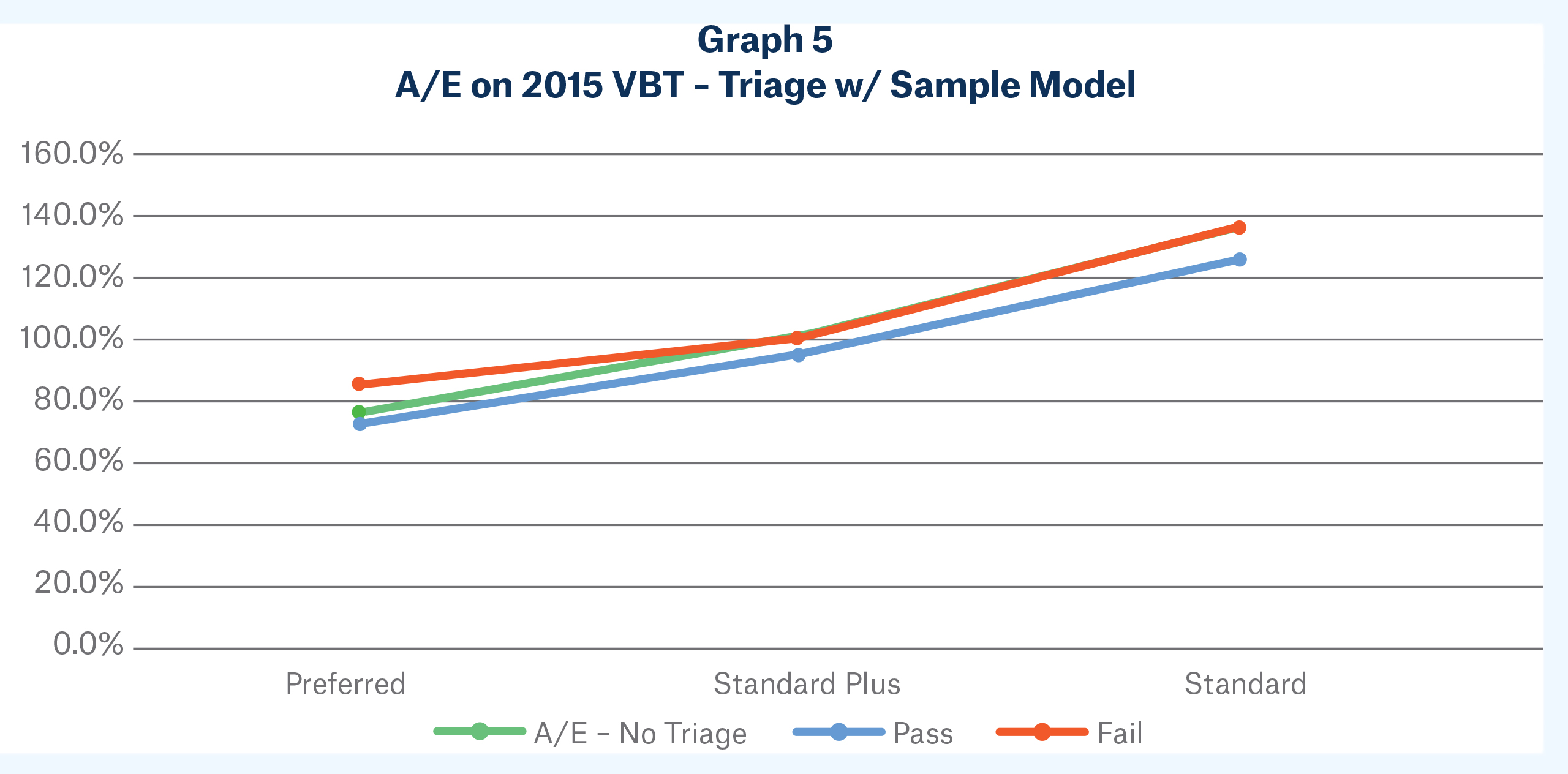
In Graph 3, A/Es relative to the 2015 VBT from the same population of about 500,000 are displayed both above and below the triage threshold. Note that the A/E vector for scores over 600 forms a nearly perfect parallel shift below the original population (labelled “No Triage”), and the vector for scores below 600 are a nearly perfect parallel shift above the original population. For this population, LNRC doesn’t just segment mortality within each class, it does so nearly identically between classes. Large mortality shifts are present on each side of the triage, but distribution shifts are immaterial. Keep in mind, though, that this result is due to the relationship between LNRC and the specific preferred criteria used to segment the test population5.
Extreme 2: The triage model and the preferred rules are highly correlated
Some life insurance companies’ proprietary models segment mortality and classify risks similarly to their traditional underwriting. This is often by design, as sometimes companies calibrate their triage model criteria to mimic their traditional underwriting criteria. If done successfully, this would lead to a triage model that is highly correlated with traditional underwriting. This means minimal to no path-dependent mortality discounts or loads would need to be considered relative to fully underwritten assumptions, as risk selection between this model’s criteria and preferred underwriting are by definition very similar. Distribution shifts, however, should be considered. The point of a triage model is to separate good risks from bad; if a triage model’s criteria are highly correlated with preferred underwriting, it will categorize traditional preferred risks as “good risks,” meaning a disproportionate number of preferred risks will be sent down the accelerated underwriting path. As a residual effect, a disproportionate number of standard risks will be sent down the traditional underwriting path. This relationship can be seen in Graph 4 on the next page, which displays class distribution shifts using a sample triage model calibrated to mimic traditional preferred criteria.
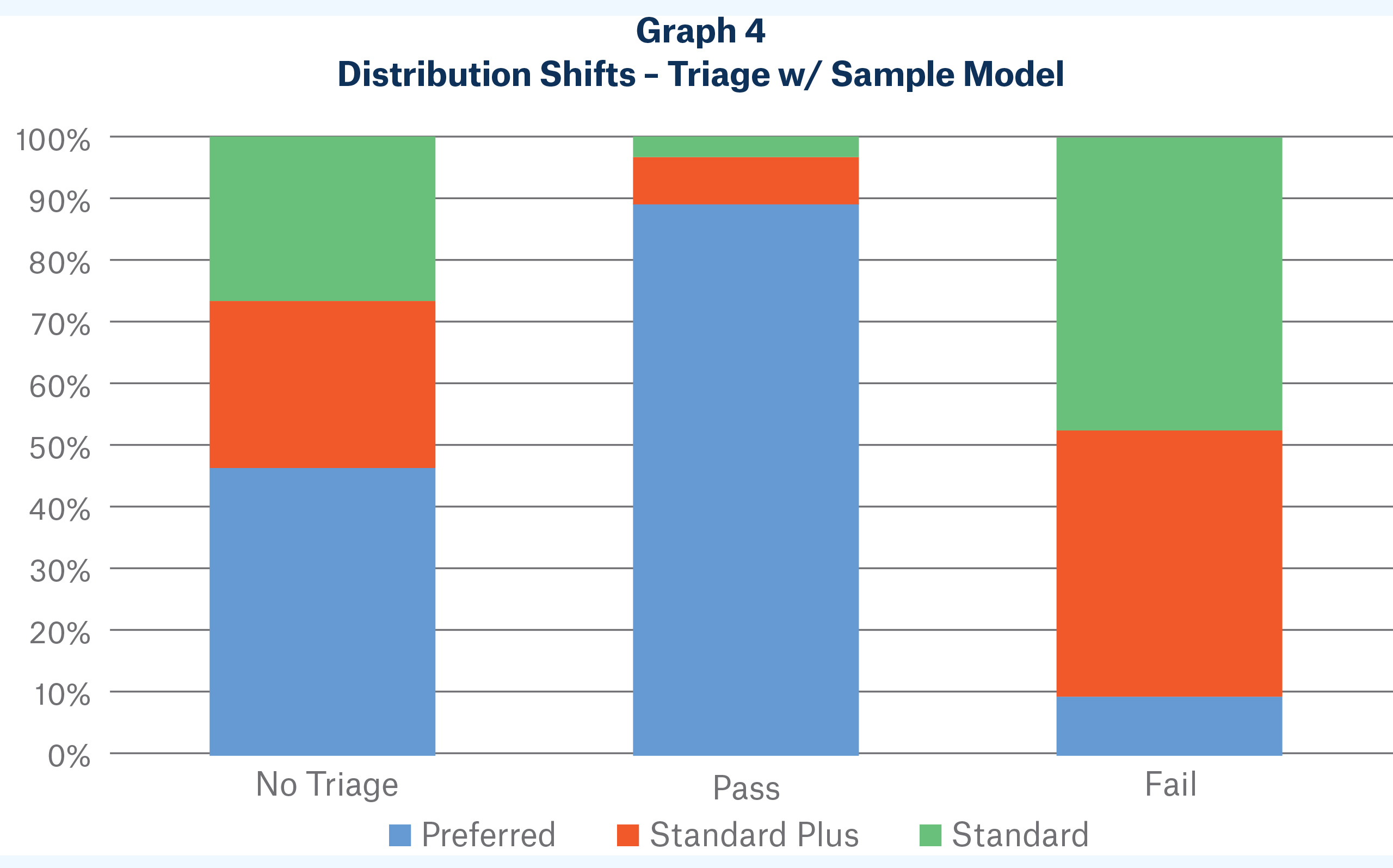
Note that the largest shifts from the “No Triage” vector come from the exceptional cases –
preferred risks which fail the model and standard risks which pass the model. With few exceptions (which make up a small distribution), A/Es segmented by this triage model are virtually the same as the A/Es of the original population. For this highly correlated extreme, large distribution shifts are present on each side of the triage, but shifts in risk class mortality are small.
These two extremes above are bookends, but uncommon in reality. Most triage programs seem to fall between the two. Typically, material mortality and prevalence shifts should be expected and each should be priced for, as each can independently affect a program’s profitability. This is important to note, as the effects of mortality shifts are obvious, whereas the effects of distribution shifts can be overlooked.
The potential impact of prevalence shifts on profit margins
Let’s assume for now that we expect overall mortality between the two triage paths to be equal in a given program. Let’s also assume that premium rates are not differentiated by triage path. It might be tempting to assume that since overall mortality is the same and premium rates are the same, then the profit margin is the same for the two paths. This does not necessarily follow.
First, prevalence could shift toward the best class. If the underwriting rules are slightly looser on one side of the triage, then overall premium collected will be less from that path than from the other path, if we held the applicants constant on both sides.
Second, overall mortality can be preserved even though risk class relative mortality and risk class prevalence could both shift. Consider the following example:
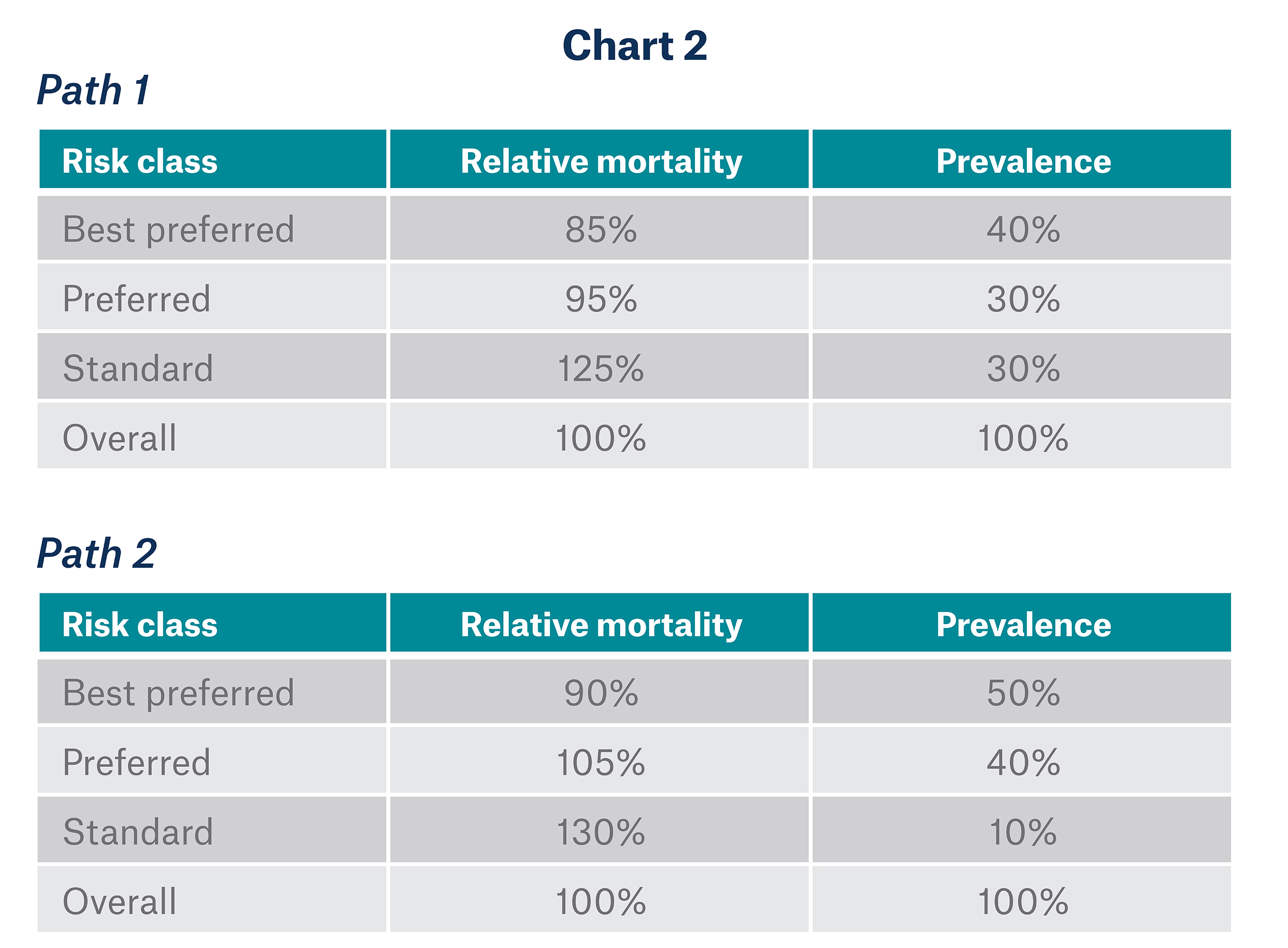
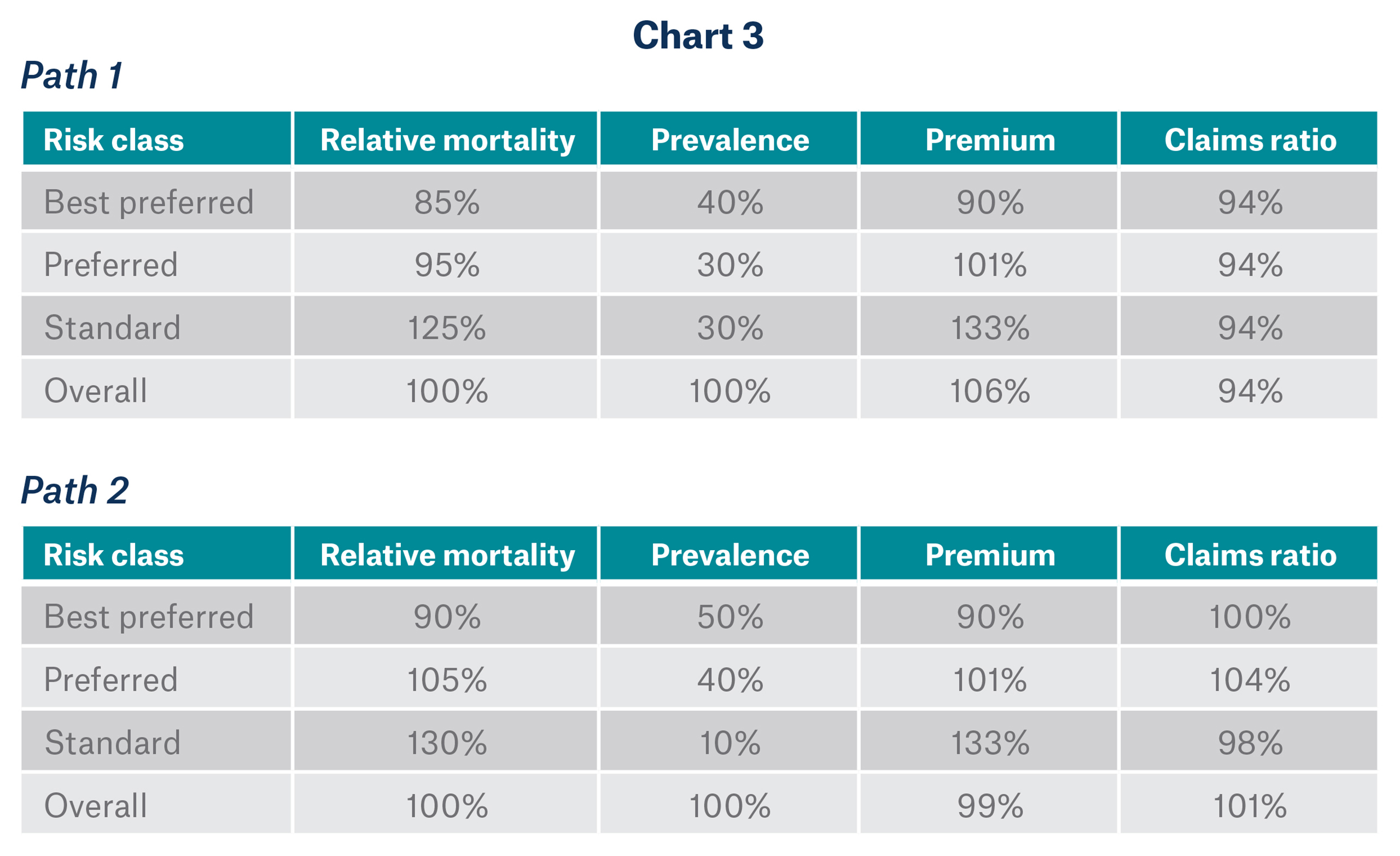
Conclusion
Triage systems within accelerated underwriting programs can impact both class prevalence and mortality, and both of these effects should be considered in pricing. Each can independently impact profitability, and ignoring either one in pricing could compromise the viability of a program. Munich Re offers clients assistance in evaluating and setting assumptions for their accelerated underwriting programs as well as in monitoring random holdout and post-issue reviews.
/Tim%20Morant.jpg/_jcr_content/renditions/original./Tim%20Morant.jpg)
